Tính diện tích xung quanh hình nón cụt, Diện tích toàn phần hình nón cụt

Tính diện tích xung quanh hình nón cụt, Diện tích toàn phần hình nón cụt là gì? Vậy bạn đã biết được những gì về công thức tính thể tích hình nón cụt? Hãy cùng đi xem và ôn lại kiến thức nhé.

Xem ngay:

• Công thức tính thể tích hình nón cụt
• Công thức tính diện tích hình tròn
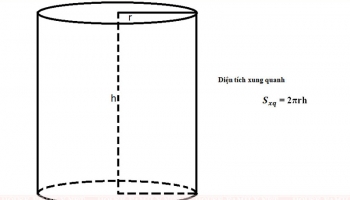
• Công thức tính diện tích xung quanh hình trụ

Hình nón cụt là gì?

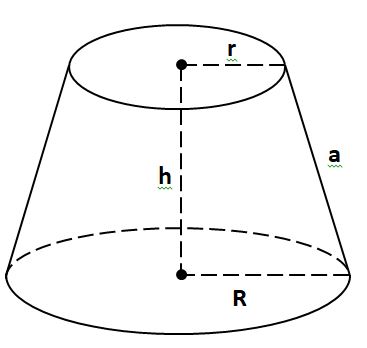
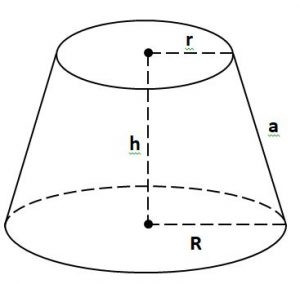
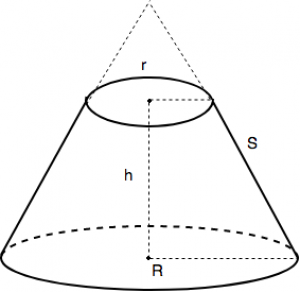
– Khi cắt hình nón bởi một mặt phẳng song song với đáy thì phần mặt phẳng nằm trong hình nón là một hình tròn. Phần hình nằm giữa mặt phẳng nói trên và mặt đáy được gọi là một hình nón cụt.

– Có thể hiểu, hình nón cụt là hình có 2 đáy là hai hình tròn có bán kính to nhỏ khác nhau nằm trên hai mặt phẳng song song có đường nối tâm là trục đối xứng.

Công thức tính diện tích xung quanh hình nón cụt

– Diện tích hình nón cụt thường được nhắc đến với 2 khái niệm: diện tích xung quanh và diện tích toàn phần.

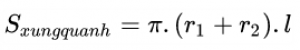
=> Trong đó:

• S_{xung quanh} : là diện tích xung quanh hình nón cụt.
• r1 và r2 : là bán kính 2 đáy của hình nón cụt.
• l : là độ dài đường sinh của hình nón cụt.
• π : số Pi (3.14159265).

Ví dụ:

– Cùng áp dụng với bài toán trên, ta có cách tính diện tích xung quanh hình nón cụt được áp dụng theo công thức sau: r1 = 5cm , r2 = 7cm và đường sinh l = 6cm.

Giải

S _{(xung quanh)} = π (r₁ + r₂)l = π(5 +7)6 = ~ 226 cm²

Công thức tính diện tích toàn phần hình nón cụt

– Diện tích toàn phần được tính là độ lớn của toàn bộ không gian hình chiếm giữ, bao gồm cả diện tích xung quanh và diện tích hai đáy tròn.

                                             Suy ra:

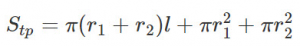
=> Trong đó:

• S_xungquanh là diện tích xung quanh hình nón cụt.
• S_toanphan là diện tích toàn phần hình nón cụt
• S_2day là diện tích 2 mặt đáy
• r1 và r2 : là bán kính 2 đáy của hình nón cụt.
• l : là độ dài đường sinh của hình nón cụt.

Ví dụ :

– Cho một hình nón cụt có bán kính hai mặt đáy r1 và r2 lần lượt bằng 5cm và 7cm. sinh l nối từ đỉnh tới đáy hình nón là 6cm. Hỏi diện tích toàn phần của hình nón này bằng bao nhiêu?

Giải

Áp dụng theo công thức tính diện tích toàn phần của hình nón cụt, ta có r1 = 5cm, r2 = 7cm và chiều dài đường sinh l = 6cm. Suy ra diện tích toàn phần của hình nón cụt khi áp dụng theo công thức như sau:

S _{(toàn phần)} = π ⋅ (r₁ + r₂) l + (π ⋅ r²₁  + π⋅ r² ₂ )

S _{(toàn phần)} = π ⋅ (5 + 7) ⋅ 6 + (π ⋅ 25 + π ⋅ 72 ) = 12 ⋅ 6 + (π ⋅ 25 + π ⋅ 49) = ~ 304 cm²

Như vậy diện tích toàn phần của hình nón cụt này bằng xấp xỉ 304 cm²